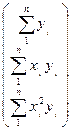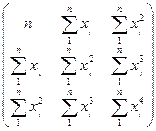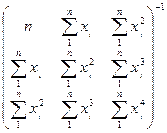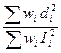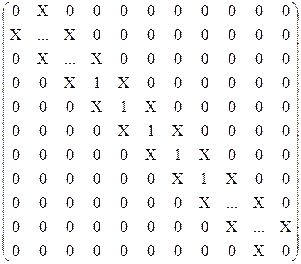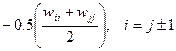Least-Squares-Refinement
| This page is currently a draft. Material may not yet be complete, information may presently be omitted, and certain parts of the content may be subject to radical, rapid alteration. More information pertaining to this may be available on the talk page. |
A short introdution from Derek Wann and Stuart Hayes:
Least-squares
processes, esd’s and correlation
1. Least-squares processes
Essentially a least-squares process involves minimising the weighted
sum of the squares of differences between observed and calculated variables, f(i):
2. Linear least squares
Consider the fitting of a polynomial to a set of n observations, y. In general the following is approximately
true,
However, the following equation is exactly true, although on its own it cannot be solved:
In order to solve it we require simultaneous equations, which are
formed by multiplying throughout by xi:
In matrix notation this is:
and can also be
written:
This is now solvable by calculating the inverse of the matrix. It
gives the values of a, b and c that fit the observations best (i.e. with the least sum of
squares of differences).
3. Non-linear least squares
We have just seen how to solve a linear least-squares problem.
Hovever, in reality many solutions cannot be obtained in this way, because the
equations are non-linear. They must be solved by an iterative process, in which
we derive shifts in parameters, which take us closer to the optimum solution.
This involves first determining the derivatives
of the observations with respect to the parameters, which may be done
analytically or numerically, depending on whether the equation can be
conveniently differentiated. In other words we gain information about how much
one observable changes when another is changed.
The mathematics of the matrix manipulations is not given here – but
as before, it involves a matrix inversion. From the results of this procedure
we obtain:
·
parameter shifts – giving better estimates of their values, ready for another
cycle of refinement.
·
an error matrix, which gives estimated standard deviations and
correlations between refining parameters.
4. ESDs
The estimated standard deviation (esd) for the mean of n observations of some parameter is 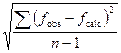 .
.
Estimated standard deviations for refining parameters are similarly
given by the error matrix.
5. R factor
We now need a way of gauging how well we are doing at minimising the
differences between the observed and calculated parameters. However, ![]() is different depending
on the magnitude of what is being measured and so comparison is not possible.
For that reason we use the following, normalising the difference term, and
comparing it to the absolute values of the measurements (intensities in
electron diffraction):
is different depending
on the magnitude of what is being measured and so comparison is not possible.
For that reason we use the following, normalising the difference term, and
comparing it to the absolute values of the measurements (intensities in
electron diffraction):
6. Data correlation
Scattering intensities lie on smooth curves, and we usually have
observations at fixed intervals (of s).
If we halved this interval, we would have more data, so our esd’s would go down
– and down, and down, and down etc. We do two things about this. First, the
intervals are chosen so that the maximum information is extracted from the
experimental data. This is a matter of trial and error, or now of experience.
Secondly, we determine a correlation parameter for a data set, which is a
measure of the extent to which any data point (or more precisely, any
difference) can be predicted from its immediate neighbours. For perfect
correlation, the value is +0.5000000…, –0.5000 would represent perfect negative
correlation, i.e. an oscillation in differences (rather unlikely). Random differences, which is what we should have, give a
value of zero. In practice anything to ±0.3 is random. If we never get values
larger than this, maybe our interval between data points is too large; if we
always get 0.49…, the interval is too small.
Once we have the correlation parameter, we use it so that account is
taken of the correlation in the data analysis. We use the weight matrix W:
where the
immediately off-diagonal points, X, are:
The diagonal terms wii
are the weighting function for the data set, rising from 0 to 1 from smin to sw1, then 1 to sw2,
and then dropping to 0 again at smax.
What we then minimise in the refinements is not ![]() =
= ![]() , but D′WD (which is identical to
what we used before, if the off-diagonal terms are zero). The R factor is then
, but D′WD (which is identical to
what we used before, if the off-diagonal terms are zero). The R factor is then ![]() , where D is the set (vector) or differences
and I
the set of intensities.
, where D is the set (vector) or differences
and I
the set of intensities.
7. Least-squares correlation
Two parameters may be correlated.
For example, consider overlapping peaks in a radial distribution curve from two
similar distances. If one distance is too large then the other becomes too
small in order to compensate. These two parameters will therefore be negatively
correlated – one goes up if the other goes down.
If we also refine the average amplitude and this value is too big
(the peak is too wide) then the shorter distance will lengthen and the longer
one will shorten, so that the two sub-peaks overlap more, and thus make the
overall peak narrower again. So the mean amplitude of vibration would be
positively correlated with one distance and negatively correlated with the
other one.
We can use values from the correlation matrix to see how other
parameters should shift if we change the value of one parameter. For example, if
the correlation between par(a) and par(b) is 0.3, and
par(a) is changed by δa, then:
The least-squares correlation matrix comes from the same calculation
as the esd’s.